Various number systems being used in digital systems are:
1. Binary Number System
consists of two numbers: 0,1
2. Decimal Number System
consists of 10 numbers: 0 to 9
3. Octal Number System
consists of 8 numbers: 0 to 7
4. Hexadecimal Number System
consists of 16 numbers: 0 to 9 and A, B, C, D, E, F
A, B, C, D, E, F are the equivalents of number : 10, 11, 12, 13, 14, 15 respectively
IMPORTANT POINTS
- Computer system understands only the binary system as all the components of the computer like transistors, switches, ports, etc. work on the two-state process of On and Off.
- Decimal Number system is not conveneint to implement in digital systems as it is difficult to design an electronic equipment that can work with 10 different voltage levels.
- Advantage of using Octal and Hexadecimal number systems is:
a) easy to represent big numbers whereas representing big numbers in binary is complex.
b) Decimal system is not used to represent big numbers because conversion from binary to octal and hexadecimal is simple as compared to conversion from binary to decimal and viceversa. Also the converison from binary to decimal is not accurate.
NUMBER CONVERSIONS
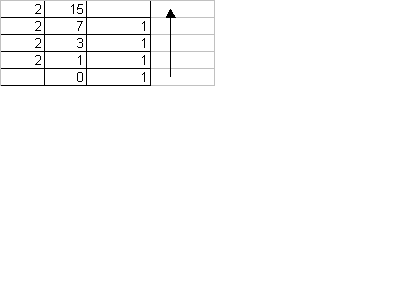
1. DECIMAL TO BINARY
Divide the integral part by the base number into which you want to convert till you get '0' as the quotient and write the remainders on the side.
Now move from bottom to top to write the remainders which is the binary equivalent of the integral number.
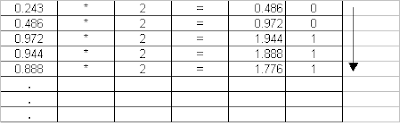
Multiply the fractional part with the base number into which you want to convert.
Write the integral value on the side and further multiply the fractional part by the base number into which you want to convert till you get '0' in the fraction.
Now move from top to bottom to write the integral values which are binary equivalent of the fractional part.
You may notice that in case of converting fractional part of Decimal system to Binary system, you may not get '0' in the final. So, you need to stop the multiplication process after 3 to 4 levels.
As a result Decimal to Binary conversion does not give you accurate results.
Example:
1. (15.25) to the base 10 into binary number.

2. (25.243) base 10 to base 2
Ans. (10001.00111) base 2
NOTE: You can see clearly in the example above that the conversion from Decimal to Binary is not accurate. For that matter even conversion from Decimal to Octal or Hexadecimal may not be accurate. This is one of the reasons for using Octal and Hexadecimal systems in Digital systems as the conversion from Decimal to Binary, Octal and Hexadecimal is not accurate.
2. DECIMAL TO OCTAL
The process of converting is the same given above for Decimal to Binary conversion. See the example below.Example: (25.650) base 10 to base 8


Ans. (31.5146) base 8
3. DECIMAL TO HEXADECIMAL
The process of converting is the same given above for Decimal to Binary conversion. See the example below.
Example: (747.03125) base 10 to base 16

4. BINARY TO DECIMAL
Pick the integer part and move in right to left direction, picking each element. Multiply each element with the base number from which you are converting to the power starting from '0' and increasing the power as you move from right to left.
Now pick the fractional part and move in left to right direction, picking each element. Multiply each element with the base number from which you are converting to the power starting from '-1' and increasing the power as you move from left to right.
Example: 11001.111 base 2 to base 10

Ans: 25.875 base 10
5. OCTAL TO DECIMAL
The conversion process remains the same as given above except that the digits will be multiplied by the base number of Octal 1.e. number 8.
Example: 352.51 base 8 to base 10

Ans. 234.64025 base 10
6. HEXADECIMAL TO DECIMAL
The conversion process is the same as above except that the digits will be multiplied by the number 16 i.e. base of the number to be converted.
Example: ABF.51 base 16 to base 10
Ans. 2752.31640625 base 10
7. BINARY TO OCTAL
Let us first write the Binary equivalents of Octal digits
0. 000
1. 001
2. 010
3. 011
4. 100
5. 101
6. 110
7. 111
NOTE: In Octal number system the numbers are to be represented in 3 bit form.
The process of conversion is as follows:
Pick the integer part and move from right to left making groups of 3. If the digits are less then add 0's to the left hand side.
Pick the fractional part and move from right to left and make groups of 3. If the digits are less then add 0's to the right hand side.
Now write the Octal value corresponding to the binary groups formed.
Example:
8. BINARY TO HEXADECIMAL
Let us first write the Binary equivalents of Hexadecimal digits
0. 0000
1. 0001
2. 0010
3. 0011
4. 0100
5. 0101
6. 0110
7. 0111
8. 1000
9. 1001
10. ( A ) 1010
11. ( B ) 1011
12. ( C ) 1100
13. ( D ) 1101
14. ( E ) 1110
15. ( F ) 1111
NOTE: In Hexadecimal number system the numbers are to be represented in 4 bit form.
The process of conversion is as follows:
Pick the integer part and move from right to left making groups of 4. If the digits are less then add 0's to the left hand side.
Pick the fractional part and move from right to left and make groups of 4. If the digits are less then add 0's to the right hand side.
Now write the Hexadecimal value corresponding to the binary groups formed.
Example:
 Ans: AE.5C base 16
Ans: AE.5C base 169. OCTAL TO BINARY
Pick each digit from the number and Simply write the binary equivalent ( represented in 3 bit form ) of the digit given.
Example:
Ans. 101100011001.100111010 base 2
10. HEXADECIMAL TO BINARY
Pick each digit from the number and Simply write the binary equivalent ( represented in 4 bit form ) of the digit given.
Example:

Ans: 0 0 1 0 1 0 1 1 1 1 1 1 . 0 1 0 1 1 1 0 0 base 2
11. OCTAL TO HEXADECIMAL
12. HEXADECIMAL TO OCTAL



1 comment:
this is really helpful
Post a Comment